Types of Trees
1. Binary Trees
Each node has at most 2 children.
Height = log2n for n number of nodes.
Types of Binary Trees
- 1. Full / Proper BT / 2-Tree
Every node have 0 or 2 children. No node have 1 child
a
/ \
b c
/ \
d e
- 2. Complete BT
All levels are completely filled except last.
a a [Not CT]
/ \ /
b c b
/ \ / /
d e f c
- 3. Perfect Tree
A full & complete BT. All leaves at same level.
a(Perfect) a(not perfect)
/ \ /\
b c b c
/ \ / \ /\ /
- 4. Balanced BT
In a balanced binary tree, the height of the left and the right subtrees of each node should vary by at most one.
Eg: AVL Tree and a Red-Black Tree
- 5. Degenerate / Pathological BT
Every internal node has only a single child. Such trees are similar to a linked list performance-wise.
a
/
b
/
c
\
d
- 6. Rope / Cord
BT where:
non-leaf node holds : sum of lengths of all leaves in left subtree
leaf node holds : string+length(also called weight)
Storing: "Hello_my_name_is_Amit"
H e l l o _ m y _ n a m e _ i s _ A m i t
0 1 2 3 4 5 6 7 8 9 1011121314151617181920
21
/
9
/ \
6 6
/ \ / \
Hello_,6 my_,3 2 1
/ \ / \
na,2 me_i,4 s,1 _Amit,5
Advatanges:
1. Used for efficient storage and manipulation a very long string.
2. Unlike arrays, ropes do not require large contiguous memory allocations.
3. Time Complexity (for insertion/deletion/searching) is O(logn) unlike strings which is O(n). Hence its VERY IMPORTANT TO LEARN.
Disadvatanges:
1. Complex code
2. Extra memory required to store parent nodes.
3. Time to access ith character increases. In plain strings its O(1).
2. Binary Search Trees (BST)
- Mainly used for Searching. Duplicate elements cannot exist. - Left-child < parent, right-child > parent. Insert/search/delete: O(log(n))
2
/ \
1 3
Types of Binary Search Trees
- 1. Self Balanced / Height Balanced BST(HBT)
- HBT always keeps itself balanced by rotation if its Balancing Factor is not equal to -1,0,1.
- BF = Right_Height - Left_Height. //if bf>2 rotation is needed
- Complexities: Insert/delete/search O(logn) even in worst case
Problem with BST?
BST may not be balanced all times, BF depends on incoming data in Real time.
[t = 1. data=9]
[t=2 data=8]
[t=3 data=7]. Instead of BST linear array is created.
9
/
8
/
7
Not Balanced. Need rotation at this node
3 (bf:-2)
/
2(bf:-1)
/
1(bf:0)
HBT
5(bf: -1)
/ \
(bf: -1)4 6(bf: 0)
/
3(bf: 0)
Rotation Examples in AVL Tree a. Left & right rotation: Similarly we can perform right,left rotation.
6 6
/ /
3 --> 4 --> 4
\ / / \
4 3 3 6
Each node have color(red or black).
struct node{
int item;
enum{red, black}color;
struct node *parent, *left, *right;
};
|
|item|color|*left|*parent|*right|
/ \
- Node is inserted based on bst if (node>root) right else left. After insertion Rules to check RBT.
- Rules of Insertion
1. If tree is empty add a black node.
2. Insert new leaf node as Red.
2a. 2 adjacent Red Nodes
Create RBT using 1,2,3,4,5,6,7,8
Rule-1 Rule-2 Rule-2
1,B -> 1,B 1,B
\ -> \
2,R 2,R
\
3,R //Voilates a. Two adjacent
Red not allowed.
a. Each node has color either red or black.
b. Root is always black.
c. 2 adjacent red nodes Not Allowed. 2 adjacent black nodes allowed. ie No Red-Red parent child relationship.
d. Every path from a node to its leaf NULL child has the same number of black nodes.
e. Add null children at leaf. null children are always black(But donot consider null while considering rule-d).
B(not RBT B(RBT) B(not RBT, violates rule-c)
/ violates rule-d) / \ /
B R B R
/ / \ / \
B B B R R
- Sorted self-balancing search tree (might not be binary). Nodes can have more than 1 children. This makes BTree a Fat Tree
Fat Tree?
- Most of data on same level. Hence depth of tree is less wrt BST & makes efficient wrt BST
- Each node contain B-1 to 2B-1 elements in a contiguous array,
hence we need not allocate every time element is inserted & improve cache efficiency.
- Searching might become linear but its better wrt BST.
- BTree is used to store huge amount of data that cannot fit in main memory. (Eg: DB)
- BTree is better wrt Disk Access: Since DB uses B-Tree/B+Tree. Search time is still better than disk.
- Time complexity(Search, Insert, Delete): O(log n). n is no of nodes.
struct btree{
int *keys; // An array of keys
int t; // Minimum degree (defines the range for number of keys)
BTreeNode **C; // An array of child pointers
int n; // Current number of keys
bool leaf; // Is true when node is leaf. Otherwise false
}
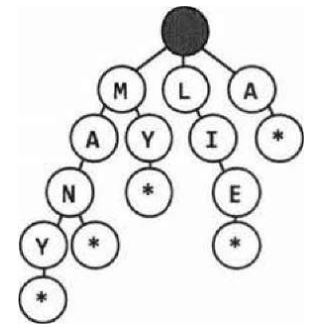
3. Trie (Prefix Tree) / Prefix tree / Digital search tree / Retrieval tree
Trie is variant of an n-arytree in which characters are stored at each node. Each path down the tree may represent a word.
Null nodes or * Nodes: are often used to indicate complete words.
Usage of Trie
- Trie is used to store the entire (English) language for quick prefix lookups.
- It can tell us if a string is a prefix of any valid words.
- Data structure used for efficient storage/retrieval/deletion of strings.
4. Heap / Binary heap / Balanced Complete BT / Priority Queue
- Each element is given a priority. Higher priority element is processed before any lower priority element.
- Duplicates are allowed. This is suited to be stored in array ie Heap can be implemented using arrays.
If you use arrays to implement Heaps then you don’t need to store pointer as done in trees and its
space advantage
Complexities
Insert: O(logn), Search: O(1), Delete: O(logn)
Types of Heap
- 4a. Max Heap
Root is always greatest. parent >= child
2nd, 3rd largest element are direct children of root(either left or right).
Traverse array and create Level-Order tree.
Heapify only non-leaf nodes. Indexes of non-leaf nodes = 0 to (N/2 - 1)
Heapfiy a node means, exchange node with either left or right child who is greatest and do till leaf node
a[] = {1, 3, 5, 4, 6, 13}
N=6. N/2-1 = 2. Need to heapify elements at index=0,1,2. Start from index=2
1 1
/ \ / \
3 5 => 6 5
/ \ / /\ /
4 6 13 4 3 13
Heapify=3
1 1
/ \ / \
6 5 => 6 13
/ \ / / \ /
3 4 13 3 4 5
Heapify 5
1 13 13
/ \ / \ / \
6 13 => 6 1 => 6 5
/ \ / / \ / / \ /
3 4 5 3 4 5 3 4 1
Heapify 1
- Max Heap of `pairs`: Elements are sorted as per values.
<2,gggg> <2,bb> <2,c> <2,aaaa>
<2,gggg>
/ \
<2,bb> <2,c>
/
<2,a>
Always insert element at bottom rightmost spot so as to maintain the complete tree property.
Insert 10
13 13
/ \ / \
6 5 => 6 10
/ \ / \ / \ /\
3 4 1 10 3 4 1 5
Swap 5,10 Until 10 finds correct spot
a[] = {13,6,5,3,4,1,10}. N=7. N/2-1 = 2. Heapify=0,1,2. Start from element at index=2
13 13
/ \ / \
6 5 => 6 10
/ \ / \ / \ / \
3 4 1 10 3 4 1 5
Heapfiy 5. index=2 heapified
index=1 a[1]=6. Donot need heapification
index=0 a[0]=13. Donot need heapification
Delete root
13
/ \
6 10
/ \ / \
3 4 1 5
Step-1. Replace last leaf node with root & Delete last node
5 5
/ \ / \
6 10 => 6 10
/ \ / \ / \ /
3 4 1 13 3 4 1
Heapify non-leaf nodes (5,6,10)
10,6 donot need heapification
5 10
/ \ / \
6 10 => 6 5
/ \ / / \ /
3 4 1 3 4 1
Heapify 5
- 4b. Min Heap
Root is always least. Condition: parent =< child. Heapify only non-leaf nodes
5. Ternary Search Tree
A tree data structure used for storing a dictionary of words where each node represents a character.
Allows for efficient searching, insertion, and deletion of strings.
6. Splay Tree
A self-adjusting binary search tree where recently accessed elements are moved to the root to optimize future accesses.
Typically used in scenarios where data access is not uniform.
7. Suffix Tree and Suffix Array
Data structures used for efficient substring search in a string or document.
Used in string processing and bioinformatics applications